(metaphysics in sense: fundamental rules, abstractions from reality, and also the negative aspect of complexity)

Paths

Unlike a road that can be abstracted entirely by a line, buildings consist mostly of congruent spaces that we move through. The road is a space too, but culturally it has been acceptable to represent the path a road takes as a line.

This leads to a problem when it comes to drawing the paths through a building; where a corridor could reasonably be represented as a line in the same way as a road, how do we represent the paths through an atrium?

The level of detail the mapper provides is part of the decision that needs to be made too, if the mapper knows the positions of all of the fixed pieces of furniture in a room for example an attempt at creating ‘virtual hallways’ might be possible (paths between tables, chairs, dividing walls). However in our case we only have a floor plan that represents the most basic elements of the building.

In this case the approach we need to take is to provide users with more in the way of ‘hints’ of where they are going in the space rather than direct instructions a la outdoor road & path mapping software.

Ideally a path that is annotated in a building represents a real path a real human might choose to take rather than a prescribed one that is created by someone looking at a floor plan or even trying to imaging how a person may choose to move through the building.

Area-based routing

Partitioning existing polygon with paths across them automatically, algorithms exist that can do this and have been investigated with pedestrian routing in mind also.

Another option is to route using one of these methods to start off with and observe how people move through the building then adjust paths. They should be adaptive! Layouts of a building change over time, they are not static, buildings are living.

Various methods can be used to divide up open space, from the more computationally simple to a better approximation of how people are actually moving. The simplest is using the exterior edges of a polygon. Another approach is to uniformly sub-divide the paces which leads to a grid structure that can approximate paths using uniform straight lines. There are a couple of computational geometry methods like the skeleton (see below) or the Voronoi diagram (which is similar) but a promising method is definitely that of the visibility method, as it seems to produce paths that we would fine ‘efficient’.

The image below has an example of this but I think more could be done to improve it, namely splitting edges on overlap so that you are always moving towards something that is visible from that point but is still efficient when it might come to change course. Overall plain visibility graphs seem to generate paths with the shortest distance (since they are by definition straight lines from point-to-point).

Of course there might still be formal paths through an open space that need to be captured, perhaps some dividing walls effectively form corridors, ‘linearising’ the space (again, see below). Or even just that there are some paved paths that jut into the space that are probably preferable to walk on compared to the mud: these should be taken into account too.

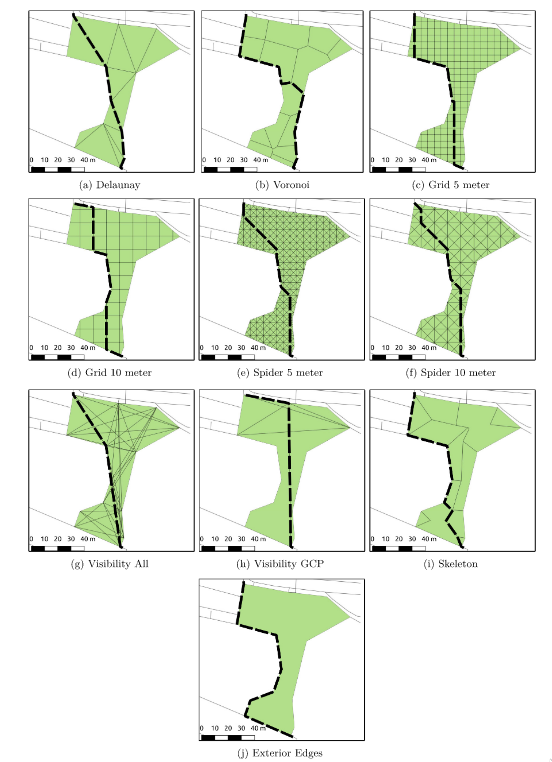
Routing examples using different algorithms (location: Weisenhausplatz, Pforzheim in Germany). (from https://doi.org/10.1080/10095020.2017.1399675)

Some papers (p. 221) model spaces as a cost surface for which a minimisation algorithm could be executed against. This would fit with the idea of having statistical distributions of where people walk and finding the minimum based on this.

Hallways

Hallways are a special case of ‘area’ since they are the only thing in buildings that approach a formal path. Whilst hallways tend to have more in them that can be interacted with than a car driving down a road they are still largely ‘paths’ that are linear. For this we can try to find an algorithm that represents them as lines, the literature refers to this as ‘collapsing’ generally as the maps wish to display these polygons as straight lines when zoomed out far enough. However these algorithms are useful for deriving ‘centerlines’ for the paths.

Haunert & Sester (2008) suggests a straight skeleton based model for collapsing sufficiently narrow areas into straight lines; for example: hallways. They assign the areas that are collapsed into lines to neighbouring areas. Whilst useful for larger geographical applications this is not really relevant in buildings are often areas are delimited by the walls and doors rather than outdoors where areas are a little less well defined generally, and the relative size of an ‘area’ to a ‘path’ is generally a lot larger.

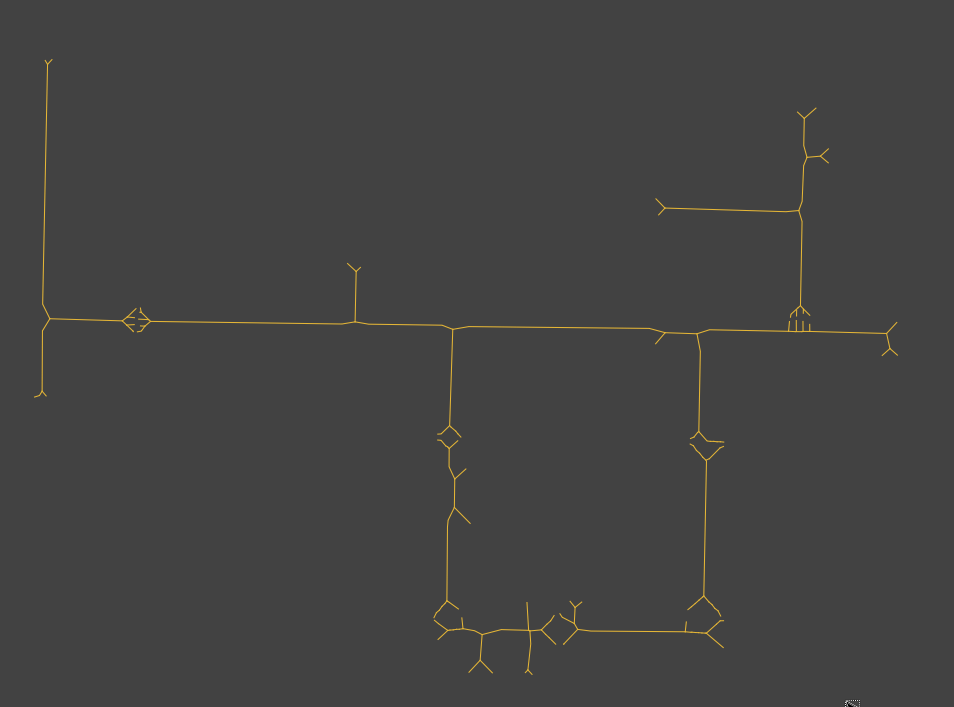
Using just the ‘skeleton’ algorithm for hallways

View of hallways

This is fine for hallways and works to simplify their navigation but also leaves long stretches between each junction that have no navigation information. Tagging points along the corridor is a decent idea and creating paths to them as junctions would work but it’s unclear how we could use this skeleton example for anything more than just the centerline. We can probably assume in this case that a straight line can be drawn from e.g. a door bordering a hallway to the centerline.

We then come to the problem of ‘bordering’, what does it mean exactly? We can use mathematics to say that a point is on a border but maps are often imperfect so the door will either be in one polygon or another, we’d need to define some sort of border radius which then becomes a lot more complex.

Navmesh

Another, completely different solution for this problem would be to consider the polygons of a building as part of a ‘navigation mesh’ (navmesh). This is a solution often used in video games where the area is decomposed into convex polygons which guarantees there is a straight-line path between any two points in the polygon (see: the definition of convex). Adjacent polygons are then connected in a graph, this means that locally we can move in a straight line through the polygon, and only globally we use a graph-search algorithm like A* to navigate. This has the benefit of reducing greatly the cost of pathfinding.

However there still would need to be a check with the underline room-defined polygons here, to generate instructions we would need to first generate the path using the navmesh then check at each point what room the user is in, overall this would complicate some parts of the program that were trivial in the area-based routing solution since you remove the ability to assign each path node a room ID that it is in.

Real Life Examples

Desire Paths

The only way to see how people naturally walk in a casual sense. Outdoors is affected by a lot more in the way of terrain, topology of the land, features etc. but it shows the path that people take without any formal guidance. This has been used by countless papers and real-world properties to determine where formal footpaths need to go.

OSM has a tag: "informal"=>"yes” for desire paths.

Obviously drawing just a path is still a reduction of a complex phenomena, perhaps they would be better represented with a Gaussian distribution but that makes route-finding very difficult. Similarly, this distribution will change with the weather and the season: if a path gets very muddy it will likely get wider as people avoid the central muddy parts.

Of note is the grass deterioration in Animal Crossing games, a much maligned feature can perhaps help to simulate how desire paths are actually formed by users. The feature was added to simulate desire paths but is too aggressive in most player’s opinion leading to a creeping desertification of frequently-traversed areas.

Red circle: visible target for people to walk towards

Red area: spectrum of paths walkers take to reach the other side of the park

Figure 1

Figure 2

Figure 3

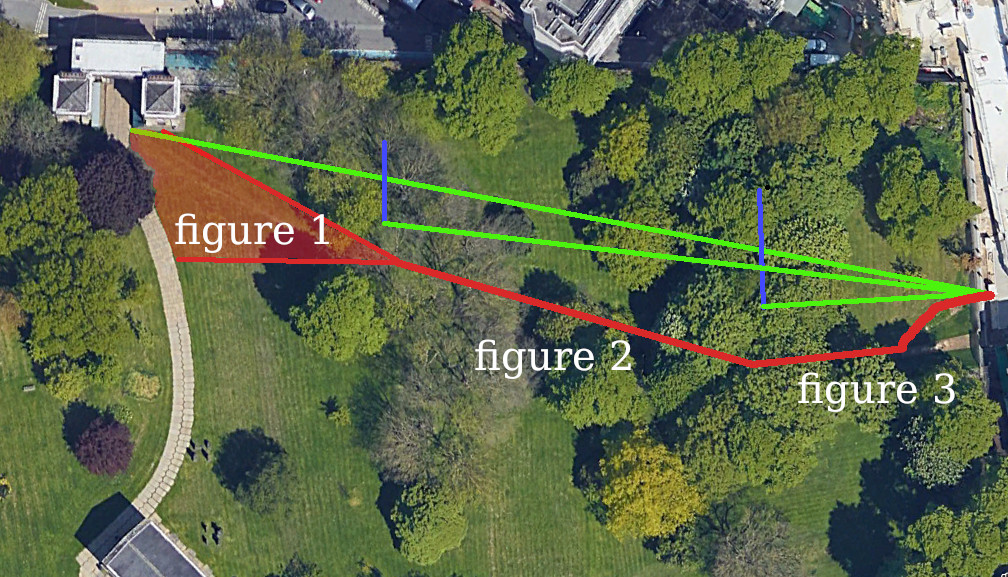
Overview of St George’s Field (Google Earth)

Figure 1:

• Green line represents the way to the exit ‘as the crow flies’ People walk in a
• rough area (with some defined paths) until they can see the bin

Figure 2:

• Having spotted the bin, people head towards that where the paved path starts

Figure 3:

• The path doesn’t lead to the exit, but instead against a wall People deviate
• from the path before the tree to exit the field Some people go around the
• front of the tree some people around the back

Stairs

Stairs are probably the trickiest thing to represent with existing techniques, there’s no real abstraction for them that isn’t somewhat clunky.

OSM Method

The OSM indoor tagging has a stairs field with a level field such that

• level=2;3;4 represents a feature that is on floor 2, 3, and 4 level=2-4 is
• the same

However this doesn’t actually say that floor 3 is accessible from this staircase.

The OSM wiki is still very much a draft on this tagging, and the way that staircases are connected isn’t clear. I believe that it implies that staircases should have doors at the start of them and these doors are what get connected between floors. Even if there is no door the door=no tag should be set.

Our Solution

Our solution was to create use the room ranges and connect every path node in them according to the type of inter-floor connection. i.e. staircases connect to the floor immediately above and below them and lifts create a fully-connected graph in their polygon (since you can travel to an arbitrary floor)

This also fixes the problem of a staircase passing a floor with no exit since we can place a singleton path node in the staircase polygon on that floor and therefore path to / from it but not have to worry about connecting it to the graph on that floor.

Ultimately this doesn’t really replicate the direction of travelling though a staircase very well but is a decent enough abstraction since the need for particular guidance on how to climb up a set of stairs isn’t needed, they are an element in a building that is linear.

Limitations

This is still a strange and incomplete abstraction for floors and inter-floor connections since the definition of a floor is actually very vague. We could be overly precise and say that any change in elevation in a building through the use of some device we can tag (stairs, lift, ramp, etc.) is a new level, using fractional floors to represent each of them, but would people consider a single step a new floor? How about a small mezzanine between levels? Clearly there’s a heuristic which people apply that is more abstract than just this. Obviously the mapper should use their better judgement but limiting the use of the stairs tag to just between-floor connections is a problem for accessibility in this case. Clearly this is a problem that needs to be considered on a per-building and by-use-case basis.

Conclusions

Overall the mapping and representations of interiors present a different set of challenges than that of mapping the outdoors. Buildings are a space that are created entirely for humans to exist in and have properties that can be abstracted away in the outdoors. To map a building is to lose some of what makes it a ‘space’ instead of a series of rooms linked together to make it a path, partly this is why there are no real comprehensive and totally agreeable schemes for doing so (OSM’s is still a draft and incomplete). Whilst labelling rooms and stairs makes sense, the use of these elements for a real, human-centred, navigable map is not there yet.

NB: this post is about a project still ongoing but I thought I'd post my thoughts about some pie-in-the-sky ideas for it, they probably won't make it into the final result